Setup

Consider an agent embedded in an environment, with the agent described by an internal state, and the environment by an external state, undergoing the cycle:

• The environment is in (external) state \(s\).
• The system receives an observation \(o \sim p(\cdot\mid s)\) from the environment.
• Then the system updates its (internal) state (e.g. beliefs) \(h \sim p(\cdot\mid \tilde{h}, o)\), with \(\tilde{h}\) the previous internal state.
• The environment receives an action \(a \sim p(\cdot\mid h)\) from the system.
• Then the environment updates its (external) state \(s' \sim p(\cdot\mid s, a)\).
• And repeat.

generating the random sequence

\[(S_1, O_1, H_1, A_1, S_{2}, \ldots)\]

which can be described by the following diagram, with the environment and agent only interacting with eachother via observations and actions

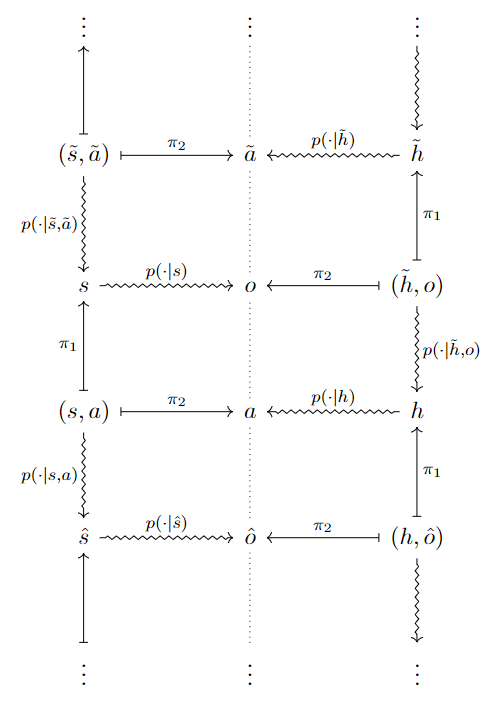
For simplicity assume action and observation distributions \(p(a\mid h)\) and \(p(o\mid s)\) are determinstic, with \(a_{\tau} = a_{\tau}(h_{\tau})\) and \(o_{\tau} = o_{\tau}(s_{\tau})\) (though with \(p(s'\mid s, a)\) and \(p(h'\mid h, o)\) stochastic).

Denote the environment state dynamics by \(\mu = \mu(s_{\tau}\mid s_{\tau-1}, a_{\tau-1}) \equiv p(s_{\tau}\mid s_{\tau-1}, a_{\tau-1})\), and the agent state dynamics (e.g. how its parameters change) by \(q = q(h_{\tau}\mid h_{\tau-1}, o_{\tau}) \equiv p(h_{\tau}\mid h_{\tau-1}, o_{\tau})\) for clarity.

At timestep \(t\) in environment \(\mu\), after experiencing the past \(\omega_t = (o_{0:t}, h_{0:t-1})\), the agent \(q\) has a preference for the future described by

\[P_t[q] := \mathbb{E}_{q}^{\mu}[\phi^t(O_{t+1}, O_{t+2}, \ldots)\mid\Omega_t=\omega_t]\]

for some \(\phi^{t}\).

• e.g. in the context of reinforcement learning we have observations \(o_{\tau} = (x_{\tau}, r_{\tau})\), with \(r_{\tau} \in \mathbb{R}\) a reward signal, with a preference that favours reward \(\phi^t(O_{t+1}, O_{t+2}, \ldots) = R_{t+1} + \gamma R_{t+2} + \gamma^2 R_{t+3} + \cdots\) for a discount factor \(\gamma\).

We will take that the agent’s internal state decomposes as \(h_{\tau} = (\theta_{\tau}, \pi_{\tau})\), with \(\theta_{\tau}\) corresponding to a parameter that updates (e.g. by gradient descent) under observation.

• e.g. \(\theta_{\tau}\) could describe synaptic weights of neurons, and \(\pi_{\tau}\) the activations/voltages across neuron synapses (plus some extra information), at time \(\tau\).

In this case we have \(q(h_{\tau}\mid h_{\tau-1}, o_{\tau}) = q(\theta_{\tau}\mid \theta_{\tau-1}, \pi_{\tau-1}, o_{\tau}) q(\pi_{\tau}\mid \theta_{\tau}, \pi_{\tau-1}, o_{\tau})\) where one can interpret \(q(\theta_{\tau}\mid \theta_{\tau-1}, \pi_{\tau-1}, o_{\tau})\) as a learning rule for the agent; how it changes its parameters under observation in order to achieve its preference. One could interpret \(q(\pi_{\tau}\mid \theta_{\tau}, \pi_{\tau-1}, o_{\tau})\) as the parameterized architecture used by the agent.

• In the context of a transformer, one could view \(\pi_{\tau}\) as the internal activations (plus some extra information), depending on the current parameters \(\theta_{\tau}\), previous activation information \(\pi_{\tau-1}\) (necessary to perform the attention mechanism) and last token \(o_{\tau}\).

Model-free credit assignment

In the parameterized view, with \(h_{\tau} = (\theta_{\tau}, \pi_{\tau})\), what is a good choice for the learning rule \(q(\theta_{\tau}\mid \theta_{\tau-1}, \pi_{\tau-1}, o_{\tau})\)?

Gradient-based learning

A common choice for the learning rule is gradient descent, with \(q = q_{\text{grad}}\), where

\[q_{\text{grad}}(\theta_{\tau}\mid \theta_{\tau-1}, \pi_{\tau-1}, o_{\tau}) := \delta\left(\theta_{\tau} - \left(\theta_{\tau-1} - \alpha \nabla_{\theta} P_t[q_{\theta}^{\tau}]\mid _{\theta = \theta_{\tau-1}}\right)\right)\]

with \(\alpha \in \mathbb{R}_{+}\) the learning rate, where \(q_{\theta}^{\tau}\) is defined such that the learning rule is turned off from timestep \(\tau\), with the parameter fixed to \(\theta\). Specifically, \(q_{\theta}^{t}\) is defined by

\[q_{\theta}^{t}(\theta_{\tau}\mid \theta_{\tau-1}, \pi_{\tau-1}, o_{\tau}) := \begin{cases} q(\theta_{\tau}\mid \theta_{\tau-1}, \pi_{\tau-1}, o_{\tau}) & \tau < t, \\ \delta(\theta_{\tau}-\theta) & \tau \geq t \end{cases}\]

It turns out that the gradient term used in this update rule, \(\nabla_{\theta} P_{t}[q_{\theta}^{\tau}]\), has a nice closed-form expression. We can write

\[\begin{align*} \mathbb{E}_{q_{\theta}^{t}}^{\mu}[\; \cdot\mid\Omega_t = \omega_t] &= \int \cdot \; p_{\theta}^{t}(s_{0:\infty}, o_{t+1:\infty}, h_{t:\infty}, a_{0:\infty}\mid o_{0:t}, h_{0:t-1}) ds_{0:\infty}, o_{t+1:\infty}, h_{t:\infty}, a_{0:\infty}\\ &= \int \cdot \; \left[\prod_{\tau=t}^{\infty} q_{\theta}^{t}(h_{\tau}\mid h_{\tau-1}, o_{\tau}(s_{\tau})) dh_{\tau}\right] [\cdots]\\ &= \int \cdot \; \left[\prod_{\tau=t}^{\infty} q(\pi_{\tau}\mid \pi_{\tau-1}, o_{\tau}; \theta) d\pi_{\tau}\right] [\cdots] \end{align*}\]

where \([\cdots]\) corresponds to factors independent of \(\theta\), and defining \(q(\pi_{\tau}\mid \pi_{\tau-1}, o_{\tau}; \theta) := q(\pi_{\tau}\mid \theta_{\tau}, \pi_{\tau-1}, o_{\tau})\mid _{\theta_{\tau} = \theta}\).

Using the fact that

\[\nabla_{\theta} q(\pi_{\tau}\mid \pi_{\tau-1}, o_{\tau}; \theta) = q(\pi_{\tau}\mid \pi_{\tau-1}, o_{\tau}; \theta) \nabla_{\theta} \log q(\pi_{\tau}\mid \pi_{\tau-1}, o_{\tau}; \theta)\]

one can then show, for inputs independent of \(\theta\), that

\[\nabla_{\theta} \mathbb{E}_{q_{\theta}^{t}}^{\mu}[\; \cdot\mid\Omega_t = \omega_t] = \mathbb{E}_{q_{\theta}^{t}}^{\mu}\left[\; \cdot \; \sum_{\tau=t}^{\infty} \nabla_{\theta} \log q(\Pi_{\tau}\mid \Pi_{\tau-1}, O_{\tau}; \theta)\mid\Omega_t = \omega_t\right]\]

It then follows that the gradient of the preference is

\[\nabla_{\theta} P_t[q_{\theta}^{t}] = \mathbb{E}_{q_{\theta}^{t}}^{\mu}\left[\sum_{\tau=t}^{\infty} \phi^t(O_{t+1}, O_{t+2}, \ldots) \nabla_{\theta} \log q(\Pi_{\tau}\mid \Pi_{\tau-1}, O_{\tau}; \theta)\mid\Omega_t = \omega_t\right]\]

reminiscent of the policy gradient theorem from RL.

We could use a Monte carlo estimator for this gradient after collecting trajectories \(\{(o_{\tau}^{(n)}, h_{\tau}^{(n)})_{\tau}\}_{n=1}^{\infty}\), i.e.

\[\hat{G}_{MC}^{t}(\theta) := \frac{1}{N}\sum_{n=1}^{N} \sum_{\tau=t}^{\infty} \phi^t(o^{(n)}_{t+1}, o^{(n)}_{t+2}, \ldots) \nabla_{\theta} \log q(\pi^{(n)}_{\tau}\mid \pi^{(n)}_{\tau-1}, o^{(n)}_{\tau}; \theta)\]

However, we can lower the variance of this estimator by using a baseline.

Reducing variance with a baseline:

One can show that

\[\mathbb{E}_{q_{\theta}^{t}}^{\mu}[b^{t}_{\tau}(\Pi_{\tau-1}, O_{\tau}; \phi) \nabla_{\theta} \log q(\Pi_{\tau}\mid \Pi_{\tau-1}, O_{\tau}; \theta)] = 0\]

for any baseline \(b^{t}_{\tau} = b^{t}_{\tau}(\pi_{\tau-1}, o_{\tau}; \phi)\), which gives us another expression for the preference gradient:

\[\nabla_{\theta} P_t[q_{\theta}^{t}] = \mathbb{E}_{q_{\theta}^{t}}^{\mu}\left[\sum_{\tau=t}^{\infty} \left[\phi^t(O_{t+1}, O_{t+2}, \ldots) - b^{t}_{\tau}(\Pi_{\tau-1}, O_{\tau}; \phi)\right] \nabla_{\theta} \log q(\Pi_{\tau}\mid \Pi_{\tau-1}, O_{\tau}; \theta)\mid\Omega_t = \omega_t\right]\]

The natural choice for the baseline would be for it to estimate \(\phi^{t}\) in some respect, however this will require predicting information about the past and future. We can restrict the baseline’s duty to just predicting the future if we assume that the preference takes a summable form:

\[\phi^{t}(O_{t+1}, O_{t+2}, \ldots) = \sum_{\tau=t+1}^{\infty} \phi_{\tau}^{t}(O_{\tau})\]

for some \(\{\phi_{\tau}^{t}\}_{\tau}\). This form is assumed for the preference unless stated otherwise. For \(\tau \geq t, \tau' \geq t+1\), it can be shown that

\[\begin{align*} &\mathbb{E}_{q_{\theta}^{t}}^{\mu}[\phi_{\tau'}^{t}(O_{\tau'}) \nabla_{\theta} \log q(\Pi_{\tau}\mid \Pi_{\tau-1}, O_{\tau}; \theta)\mid\Omega_{t}=\omega_{t}]\\ &= \int p_{\theta}^{t}(\theta_{\tau}, \theta_{\tau-1}, \pi_{\tau}, \pi_{\tau-1}, o_{\tau}, o_{\tau'}\mid \omega_{t}) \phi_{\tau'}^{t}(o_{\tau'}) \nabla_{\theta} \log q(\pi_{\tau}\mid \pi_{\tau-1}, o_{\tau}; \theta)\\ &= \int p_{\theta}^{t}(\theta_{\tau}\mid \theta_{\tau-1}, \pi_{\tau-1}, o_{\tau}, o_{\tau'}) p_{\theta}^{t}(\pi_{\tau}\mid \theta_{\tau}, \pi_{\tau-1}, o_{\tau}, o_{\tau'}) [\cdots] \phi_{\tau'}^{t}(o_{\tau'}) \nabla_{\theta} \log q(\pi_{\tau}\mid \pi_{\tau-1}, o_{\tau}; \theta)\\ &= \int \phi_{\tau'}^{t}(o_{\tau'}) q(\pi_{\tau}\mid \pi_{\tau-1}, o_{\tau}; \theta) [\cdots] \nabla_{\theta} \log q(\pi_{\tau}\mid \pi_{\tau-1}, o_{\tau}; \theta) \; \text{for} \; \tau' \leq \tau\\ &= 0 \; \text{for} \; \tau' \leq \tau \end{align*}\]

therefore the preference gradient can be written

\[\nabla_{\theta} P_t[q_{\theta}^{t}] = \mathbb{E}_{q_{\theta}^{t}}^{\mu}\left[\sum_{\tau=t}^{\infty} \left[V^{t}_{\tau} - b^{t}_{\tau}(\Pi_{\tau-1}, O_{\tau}; \phi)\right] \nabla_{\theta} \log q(\Pi_{\tau}\mid \Pi_{\tau-1}, O_{\tau}; \theta)\mid\Omega_t = \omega_t\right]\]

defining the value at timestep \(t\) from \(\tau \geq t\)

\[V_{\tau}^{t} := \sum_{\tau'=\tau+1}^{\infty} \phi_{\tau'}^{t}(O_{\tau'})\]

Then to best minimise the variance of the corresponding Monte Carlo estimator, we want \(b^{t}_{\tau}\) to estimate \(V^{t}_{\tau}\). Denoting \(b^{t}_{\tau} \equiv \hat{V}^{t}_{\tau}\) for clarity, we want

\[\hat{V}^{t}_{\tau}(h_{\tau-1}, o_{\tau}; \phi) \approx v_{\tau}^{t}\]

which can be enforced by optimizing \(\phi\) via supervised learning using collected trajectories. Such a baseline is called a value baseline.

Overall we have preference gradient

\[\nabla_{\theta} P_t[q_{\theta}^{t}] = \mathbb{E}_{q_{\theta}^{t}}^{\mu}\left[\sum_{\tau=t}^{\infty} \left[V^{t}_{\tau} - \hat{V}^{t}_{\tau}(\Pi_{\tau-1}, O_{\tau}; \phi)\right] \nabla_{\theta} \log q(\Pi_{\tau}\mid \Pi_{\tau-1}, O_{\tau}; \theta)\mid\Omega_t = \omega_t\right]\]

Advantage-based estimators:

Ignoring the baseline for a moment, see that

\[\begin{align*} \nabla_{\theta} P_t[q_{\theta}^{t}] &= \sum_{\tau=t}^{\infty} \mathbb{E}_{q_{\theta}^{t}}^{\mu}\left[V^{t}_{\tau} \nabla_{\theta} \log q(\Pi_{\tau}\mid \Pi_{\tau-1}, O_{\tau}; \theta)\mid\Omega_t = \omega_t\right]\\ &= \sum_{\tau=t}^{\infty} \mathbb{E}_{q_{\theta}^{t}}^{\mu}\left[\mathbb{E}_{q_{\theta}^{t}}^{\mu}\left[V^{t}_{\tau} \nabla_{\theta} \log q(\Pi_{\tau}\mid \Pi_{\tau-1}, O_{\tau}; \theta)\mid\Omega_t = \omega_t, \Omega_{\tau}, \Pi_{\tau}\right]\right]\\ &= \sum_{\tau=t}^{\infty} \mathbb{E}_{q_{\theta}^{t}}^{\mu}\left[\nabla_{\theta} \log q(\Pi_{\tau}\mid \Pi_{\tau-1}, O_{\tau}; \theta) \mathbb{E}_{q_{\theta}^{t}}^{\mu}\left[V^{t}_{\tau}\mid\Omega_t = \omega_t, \Omega_{\tau}, \Pi_{\tau}\right]\right]\\ &=: \mathbb{E}_{q_{\theta}^{t}}^{\mu}\left[\sum_{\tau=t}^{\infty} Q_{\tau}^{t}[q_{\theta}^{t}\mid\Omega_{\tau}, \Pi_{\tau}] \; \nabla_{\theta} \log q(\Pi_{\tau}\mid \Pi_{\tau-1}, O_{\tau}; \theta)\right] \end{align*}\]

defining the action-value at timestep \(t\) from \(\tau \geq t\)

\[\begin{align*} Q_{\tau}^{t}[q_{\theta}^{t}\mid\Omega_{\tau}, \Pi_{\tau}] &:= \mathbb{E}_{q_{\theta}^{t}}^{\mu}\left[V^{t}_{\tau}\mid\Omega_t = \omega_t, \Omega_{\tau}, \Pi_{\tau}\right]\\ &\equiv \mathbb{E}_{q_{\theta}^{t}}^{\mu}\left[V^{t}_{\tau}\mid O_{0:\tau} = (o_{0:t}, O_{t+1:\tau}), H_{0:\tau} = (h_{0:t-1}, H_{t:\tau})\right] \end{align*}\]

i.e. the expected value in the future from \(\tau \geq t\), conditioned on all past observed information from \(\tau\) and the hidden state at \(\tau\).

Then including baseline we have

\[\nabla_{\theta} P_t[q_{\theta}^{t}] = \mathbb{E}_{q_{\theta}^{t}}^{\mu}\left[\sum_{\tau=t}^{\infty} \left[Q_{\tau}^{t}[q_{\theta}^{t}\mid\Omega_{\tau}, \Pi_{\tau}] - b^{t}_{\tau}(\Pi_{\tau-1}, O_{\tau}; \phi)\right] \nabla_{\theta} \log q(\Pi_{\tau}\mid \Pi_{\tau-1}, O_{\tau}; \theta)\right]\]

Typical advantage based estimators choose a value baseline as seen in the previous section, with \(b^{t}_{\tau} = \hat{V}^{t}_{\tau}\), giving preference gradient

\[\nabla_{\theta} P_t[q_{\theta}^{t}] = \mathbb{E}_{q_{\theta}^{t}}^{\mu}\left[\sum_{\tau=t}^{\infty} A_{\tau}^{t}[q_{\theta}^{t}\mid\Omega_{\tau}, \Pi_{\tau}; \phi] \; \nabla_{\theta} \log q(\Pi_{\tau}\mid \Pi_{\tau-1}, O_{\tau}; \theta)\right]\]

defining the advantage.

\[A_{\tau}^{t}[q_{\theta}^{t}\mid\Omega_{\tau}, \Pi_{\tau}; \phi] := Q_{\tau}^{t}[q_{\theta}^{t}\mid\Omega_{\tau}, \Pi_{\tau}] - \hat{V}^{t}_{\tau}(\Pi_{\tau-1}, O_{\tau}; \phi)\]

which is the value gain due to state \(\Pi_{\tau}\) (compared to average, computed by \(\hat{V}_{\tau}^{t}\)).

How can we estimate the advantage? Note that

\[V_{\tau}^{t} =\phi^{t}_{\tau+1}(O_{\tau+1}) + \cdots + \phi^{t}_{\tau+K}(O_{\tau+K}) + V_{\tau+K}^{t}\]

for any \(K = 1, 2, \ldots\), and using

\[\mathbb{E}_{q_{\theta}^{t}}^{\mu}[V^{t}_{\tau+K}] \approx \mathbb{E}_{q_{\theta}^{t}}^{\mu}[\hat{V}^{t}_{\tau+K}(\Pi_{\tau+K-1}, O_{\tau+K}; \phi)]\]

we can bootstrap \(Q_{\tau}^{t}\) by \(K\) steps

\[\begin{align*} Q_{\tau}^{t}[q_{\theta}^{t}\mid\Omega_{\tau}, \Pi_{\tau}] \approx \; &\mathbb{E}_{q_{\theta}^{t}}^{\mu}\left[\hat{V}^{t}_{\tau+K}(\Pi_{\tau+K-1}, O_{\tau+K}; \theta)\mid \Omega_t = \omega_t, \Omega_{\tau}, \Pi_{\tau}\right]\\ &+ \sum_{\tau'=\tau+1}^{\tau+K} \mathbb{E}_{q_{\theta}^{t}}^{\mu}\left[\phi_{\tau'}^{t}(O_{\tau'})\mid \Omega_t = \omega_t, \Omega_{\tau}, \Pi_{\tau}\right] \end{align*}\]

which gives advantage

\[\begin{align*} A_{\tau}^{t}[q_{\theta}^{t}\mid\Omega_{\tau}, \Pi_{\tau}; \theta] \approx \; &- \hat{V}^{t}_{\tau}(\Pi_{\tau-1}, O_{\tau}; \phi) + \mathbb{E}_{q_{\theta}^{t}}^{\mu}\left[\hat{V}^{t}_{\tau+K}(\Pi_{\tau+K-1}, O_{\tau+K}; \theta)\mid \Omega_t = \omega_t, \Omega_{\tau}, \Pi_{\tau}\right]\\ &+ \sum_{\tau'=\tau+1}^{\tau+K} \mathbb{E}_{q_{\theta}^{t}}^{\mu}\left[\phi_{\tau'}^{t}(O_{\tau'})\mid \Omega_t = \omega_t, \Omega_{\tau}, \Pi_{\tau}\right] \end{align*}\]

Then after observing trajectories \(\{(o_{\tau}^{(n)}, h_{\tau}^{(n)})_{\tau}\}_{n=1}^{\infty}\), we have Monte Carlo estimator

\[\begin{align*} \hat{G}^{t}_{MC}(\theta) &:= \frac{1}{N}\sum_{n=1}^{N} \sum_{\tau=t}^{\infty} a_{\tau}^{t}(o_{\tau:\tau+K}^{(n)}, \pi_{\tau-1}^{(n)}, \pi_{\tau+K}^{(n)}; \phi) \nabla_{\theta} \log q(\pi^{(n)}_{\tau}\mid \pi^{(n)}_{\tau-1}, o^{(n)}_{\tau}; \theta) \end{align*}\]

with observed advantages

\[a_{\tau}^{t}(o_{\tau:\tau+K}, \pi_{\tau-1}, \pi_{\tau+K}; \phi) := -\hat{V}_{\tau}^{t}(\pi_{\tau-1}, o_{\tau}; \phi) + \hat{V}_{\tau+K}^{t}(\pi_{\tau+K-1}, o_{\tau+K}; \phi) + \sum_{\tau'=\tau+1}^{\tau+K} \phi_{\tau'}^{t}(o_{\tau'})\]

which is equivalent to gradient descent on the loss function \(L^t = L^t(\theta)\) defined as

\[L^t(\theta) := \frac{1}{N}\sum_{n=1}^{N} \sum_{\tau=t}^{\infty} a_{\tau}^{t}(o_{\tau:\tau+K}^{(n)}, \pi_{\tau-1}^{(n)}, \pi_{\tau+K}^{(n)}; \phi) \log q(\pi^{(n)}_{\tau}\mid \pi^{(n)}_{\tau-1}, o^{(n)}_{\tau}; \theta)\]

Advantage-based methods are seen to work very well in the context of reinforcement learning (PPO is an example of such a method).

Model-based credit assignment

Tree search methods

We now discuss the approach of an agent using tree search methods, guided by learned predictive models of the environment, in order to choose actions effectively. For simplicity assume a discrete finite action space of \(A\) actions.

At time \(t\) the agent has observed \(o_{0:t}\), say with parameter \(\theta\) parameterizing the predictive distributions

\[h_{\theta} = h_{\theta}(o_{0:t}) =: z^t_{0} \in \mathbb{R}^{d}\] \[f_{\theta} = f_{\theta}(z^t_{k}) =: (\mathbf{p}^t_{k}, v^{t:t+k}_{t+k})\] \[g_{\theta} = g_{\theta}(z^t_{k-1}, i) = (\psi^{t:t+k-1}_{t+k}, z^{t}_{k, i})\]

with

\[\psi^{\tau}_{t+k} \approx \mathbb{E}_{q}^{\mu}[\phi^{\tau}_{t+k}(O_{t+k})\mid\Omega_{t} = \omega_{t}]\] \[v^{\tau}_{t+k} \approx \mathbb{E}_{q}^{\mu}[V^{\tau}_{t+k}\mid\Omega_{t} = \omega_t]\]

enforced via supervised learning (discussed more below).

The tree-search agent \(q = q_{\text{Search}}\) produces its action \(a_{t}\) by the following algorithm

1. Obtain root latent state \(z^t_0 := h_{\theta}(o_{0:t})\).
2. Expand this root state into children \(\{z^{t}_{1, i}\}_{i=1}^{A}\) with \(z^{1}_{t, i}\) obtained by computing \(g_{\theta}(z_{t}^{k-1}, a_i)\).
3. Run a number of tree search simulations, with each consisting of:
   • Starting from the root, take actions \(i_{k+1} := \text{argmax}_{j} \text{UCB}(z^{t}_{k, i_{k}}, j)\) in the order \(k=0, \ldots, n-1\), until visiting a node \(z^{t}_{n}\) that has yet to be expanded.
   • Increment the visit count of the nodes visited during this simulation, \(\{z_{t}^{0}, \ldots, z_{t}^{n}\}\), and add the \(n\)-step bootstrapped value \(\hat{v}^{t+k}_{t+k} := \pm(\psi^{t+k}_{t+k+1} + \cdots + \psi^{t+k}_{t+n} + v^{t+k}_{t+n})\) to node \(z_{t}^{k}\)’s total value (initialized to \(0\)), with \(\pm\) depending on which player is moving.
4. After running these simulations, choose the next action by sampling from the distribution based on the visits to the children of the root node: \(p(i) = \left(\frac{n^{t}_{1, i}}{\sum_{j=1}^{A} n^{t}_{1, j}}\right)^{1/\nu}\) with temperature \(\nu\).

TODO

Meta-learning

At the base level, with no meta-learning, denote the hidden state \(h_{\tau} = h_{\tau}^{(0)}\) with dynamics \(q = q^{(0)} = q^{(0)}(h_{\tau}^{(0)}\mid h_{\tau-1}^{(0)}, o_{\tau})\). For example, a parameterized agent has \(h_{\tau}^{(0)} = (\theta_{\tau}, \pi_{\tau})\).

Consider a level higher, with meta-learning dynamics \(q = q^{(1)}\) with state \(h_{\tau} = h_{\tau}^{(1)} := (h_{\tau}^{(0)}, q_{\tau}^{(0)})\) and defined such that

\[q = q^{(1)}(h_{\tau}^{(0)}\mid q_{\tau}^{(0)}, h_{\tau-1}^{(0)}, o_{\tau}) = q_{\tau}^{(0)}(h_{\tau}^{(0)}\mid h_{\tau-1}^{(0)}, o_{\tau})\]

I.e. the hidden state consists of the base state \(h_{\tau}^{(0)}\) and the update rule \(q_{\tau}^{(0)}\) for this base state, and \(q^{(1)} = q^{(1)}(h_{\tau}\mid h_{\tau-1}, o_{\tau})\) governs how both this base state and its update rule are updated, allow for meta-learning of the learning rule \& architecture itself, with dynamics

\[\begin{align*} q(h_{\tau}\mid h_{\tau-1}, o_{\tau}) &= q^{(1)}(h_{\tau}^{(1)}\mid h_{\tau-1}^{(1)}, o_{\tau})\\ &= q^{(1)}(h_{\tau}^{(0)}, q_{\tau}^{(0)}\mid h_{\tau-1}^{(0)}, q_{\tau-1}^{(0)}, o_{\tau})\\ &= q^{(1)}(q_{\tau}^{(0)}\mid h_{\tau-1}^{(0)}, q_{\tau-1}^{(0)}, o_{\tau}) \; q_{\tau}^{(0)}(h_{\tau}^{(0)}\mid h_{\tau-1}^{(0)}, o_{\tau}) \end{align*}\]

Consider more generally \(\text{meta}^{K}\)-learning dynamics, for some \(K = 1, 2, \ldots\). This corresponds to dynamics governed by \(q = q^{(K)}\), with \(q^{(K)} = q^{(K)}(h_{\tau}^{(K)}\mid h_{\tau-1}^{(K)}, o_{\tau})\) with hidden state

\[h_{\tau} = h_{\tau}^{(K)} := (h_{\tau}^{(K-1)}, q_{\tau}^{(K-1)}) = \cdots = (h_{\tau}^{(0)}, q_{\tau}^{(0)}, \ldots, q_{\tau}^{(K-1)})\]

The hidden state consists of \(K\) distributions \(\{q_{\tau}^{(k)}\}_{k=0}^{K-1}\), defined such that

\[q_{\tau}^{(k)}(h_{\tau}^{(k-1)}\mid q_{\tau}^{(k-1)}, h_{\tau-1}^{(k-1)}, o_{\tau}) = q_{\tau}^{(k-1)}(h_{\tau}^{(k-1)}\mid h_{\tau-1}^{(k-1)}, o_{\tau})\]

This gives overall \(\text{meta}^{K}\) dynamics

\[q = q^{(K)}(h_{\tau}^{(K)}\mid h_{\tau-1}^{(K)}, o_{\tau}) = q_{\tau}^{(0)}(h_{\tau}^{(0)}\mid h_{\tau-1}^{(0)}, o_{\tau}) \left[\prod_{k=1}^{K} q_{\tau}^{(k)}(q_{\tau}^{(k-1)}\mid q_{\tau-1}^{(k-1)}, h_{\tau-1}^{(k-1)}, o_{\tau})\right]\]

TODO: discuss popular meta learning dynamics (MAML, etc.)

AIXI

\[\begin{align*} P_t[q] &:= \mathbb{E}_{q}^{\mu}[\phi^t(O_{t+1}, O_{t+2}, \ldots)\mid \Omega_t=\omega_t]\\ &= \int p(o_{t+1:\infty}\mid o_{0:t}, h_{0:t-1}) \phi^t(o_{t+1:\infty}) do_{t+1:\infty}\\ &= \int p(o_{t+1:\infty}, h_{t:\infty}\mid o_{0:t}, h_{0:t-1}) \phi^t(o_{t+1:\infty}) do_{t+1:\infty} dh_{t:\infty}\\ &= \int \phi^t(o_{t+1:\infty}) \left[\prod_{\tau=t}^{\infty} q(h_{\tau}\mid o_{\tau}, h_{\tau-1}) p(o_{\tau+1}\mid o_{0:\tau}, a_{0:\tau}(h_{0:\tau})) dh_{\tau} do_{\tau+1}\right] \end{align*}\]

The agent does not have access to \(p(o_{\tau+1}\mid o_{0:\tau}, h_{0:\tau})\), but lets say it has a model of this distribution, \(\hat{p} = \hat{p}(o_{\tau+1}\mid o_{0:\tau}, h_{0:\tau})\) (observations and hidden states are accessible by the agent, hence one can imagine learning such a model via supervised learning).

Define the preference under this predictive model

\[\hat{P}_{t}[q, \hat{p}] := \int \phi^t(o_{t+1:\infty}) \left[\prod_{\tau=t}^{\infty} q(h_{\tau}\mid o_{\tau}, h_{\tau-1}) \hat{p}(o_{\tau+1}\mid o_{0:\tau}, a_{0:\tau}(h_{0:\tau})) dh_{\tau} do_{\tau+1}\right]\]

The AIXI model chooses \(\hat{p}\) to be the Solomonoff prior. This can be described by \(\hat{p} = \hat{p}_{S}\) with

\[\hat{p}_{S}(o_{1:\tau+1}\mid o_{0}, a_{0:\tau}) := \sum_{\substack{\sigma\\U(\sigma, o_0, a_{0:\tau}) = o_{1:\tau+1}}} 2^{-\ell(\sigma)}\]

for some universal Turing machine \(U\), summing over programs \(\sigma\) and weighting based on program length \(\ell(\sigma)\). Under this prior we have

\[\begin{align*} \hat{p}_{S}(o_{\tau+1}\mid o_{0:\tau}, a_{0:\tau}) = \frac{\hat{p}(o_{1:\tau+1}\mid o_0, a_{0:\tau})}{\hat{p}(o_{1:\tau}\mid o_0, a_{0:\tau})} &= \frac{\hat{p}(o_{1:\tau+1}\mid o_0, a_{0:\tau})}{\int do'_{\tau+1} \hat{p}(o_{1:\tau}, o'_{\tau+1}\mid o_0, a_{0:\tau})}\\ &= \frac{\sum_{\sigma: U(\sigma, o_0, a_{0:\tau}) = o_{1:\tau+1}} \; 2^{-\ell(\sigma)}}{\int do'_{\tau+1} \sum_{\sigma': U(\sigma', o_0, a_{0:\tau}) = (o_{1:\tau}, o'_{\tau+1})} \; 2^{-\ell(\sigma')}} \end{align*}\]

TODO: finish AIXI, discuss generalization from the perspective of Kolmogorov complexity